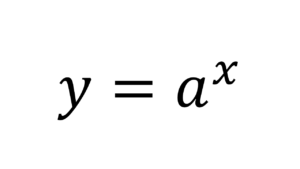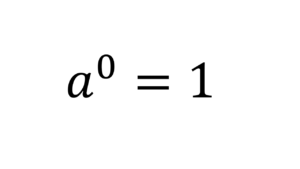確率1%は100回やったら100%になるのか? 【理系雑学】
「確率1%だから、100回やったら確率的には100%だ!」
って感じの話、定期的に出ません?
結論から言うと、実は確率的には63%くらいなんです。
どうでしょうか、結構低い感じしますよね。
今回はそんな確率に関してご紹介していきます。
確率の基本
確率は中学数学で基本的なところを学びますが、使わないと忘れちゃいますよね。
なのでまずは簡単に、確率についておさらいしていきましょう。
%(パーセント)と百分率
確率は「%(パーセント)」の他に「百分率」という形でも表せます。
%と百分率の関係としては
$$1\%=\frac{1}{100} $$
です。ですので、百分率に$\times100$してあげれば%に直せます。
確率の求め方
続いては確率の求め方ですが、これは
$$確率=\frac{確率を求める場合の数}{起こりうるすべての場合の数} $$
で求められます。
例えばコイントスをして表が出る確率を考える場合、コインの出方は表と裏の2通りなので確率は
$確率=\frac{確率を求める場合の数(表の1通り)}{起こりうるすべての場合の数(表と裏の2通り)}= \frac{1}{2}$
となります。これを%に直すと
$$\frac{1}{2}\times100=50\%$$
となり、コインの表が出る確率は50%ということがわかります。
また、確率は最小0%(百分率で0)、最大100%(百分率で1)です。
ちなみにちょっとわき道にそれますが、200%とかも聞くけど違うの?と思われるかもしれません。
あれは確率じゃなくて比率になります。
例えば「確率200%UP」は「確率が2倍」という意味です。
確率の組み合わせ
確率の組み合わせは掛け算で行うことができます。
例えばコイントスで2回連続で表が出る確率を求めるとします。
先ほどの例で表が出る確率は$\frac{1}{2}$ということが分かっているので、表が2回連続で出る確率は
$$\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}$$
となります。(パーセントに直すと25%)
○○でない確率
続いては今回の内容に直結する「○○でない確率」の考え方です。
これは
$$1-○○である確率=○○でない確率$$
で求められます。
例えば5つの箱があって、その中の1つだけに景品が入っている場合を考えましょう。
挑戦者はその中から1つだけを選んで、景品が入っている場合はそれをもらえます。
先ほどまでと同じ考え方を使うと、挑戦者が景品を当てられる確率は$\frac{1}{5}$です。
それでは当てられない確率を考えると、先ほどの式に当てはめて
$$1-\frac{1}{5}=\frac{4}{5}$$
となり、$\frac{4}{5}$と求めることができます。(パーセントに直すと80%)
確率1%は100回やったら100%になるか
それでは本題の「確率1%は100回やったら100%になるか」に入っていきます。
進め方としては、今までの内容を組み合わせて
1-100回やっても1回も当たらない確率=100回やって1回以上当たる確率
という形で求めていきます。
なぜこんな回りくどいやり方をするかというと、100回やって1回以上当たる確率というのは
100回やって1回以上当たる確率=1回当たる確率+2回当たる確率+ …+100回当たる確率
という風にすべての当たる確率を足さないといけないからです。
でもめんどくさいですよね。
なので、まずは100回やっても1回も当たらない確率を求めます。
当たる確率が1%ということは、言い換えれば当たらない確率は99%ということになります。なので百分率に直すと$\frac{99}{100}$となります。
これを100回組み合わせればよいので、$\frac{99}{100}$を100回かけることになります。
そうすると
$$(\frac{99}{100})^{100}=0.366032341273229$$
と出てきます。
これを用いて100回やって1回以上当たる確率を求めると
$$1-0.366032341273229=0.633967658726771$$
となります。
すなわち当たりが出る確率が1%のものを100回やって1回以上当たりが出る確率は約63%ということになります。
じゃあ何回くらいでほぼ100%になる?
100回やっても63%ということがわかりましたが、では何回くらいでほぼ100%になるのかを見ていきましょう。
1000回までやった場合に1回でもあたりが出る確率は下のグラフのように推移します。
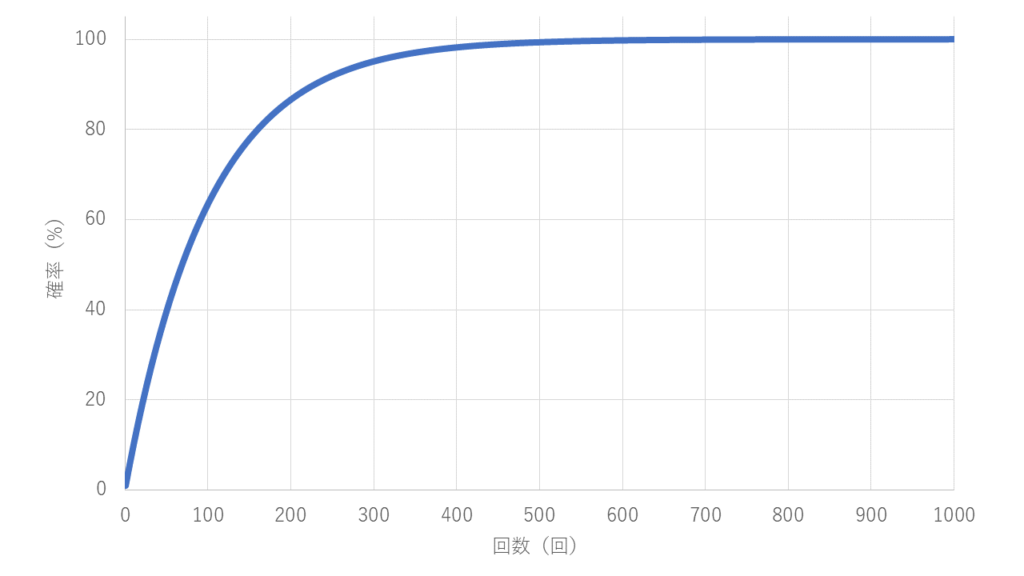
400回あたりで100%にかなり近くなっているような気がします。
100回ごとの確率は下の表のようになります。
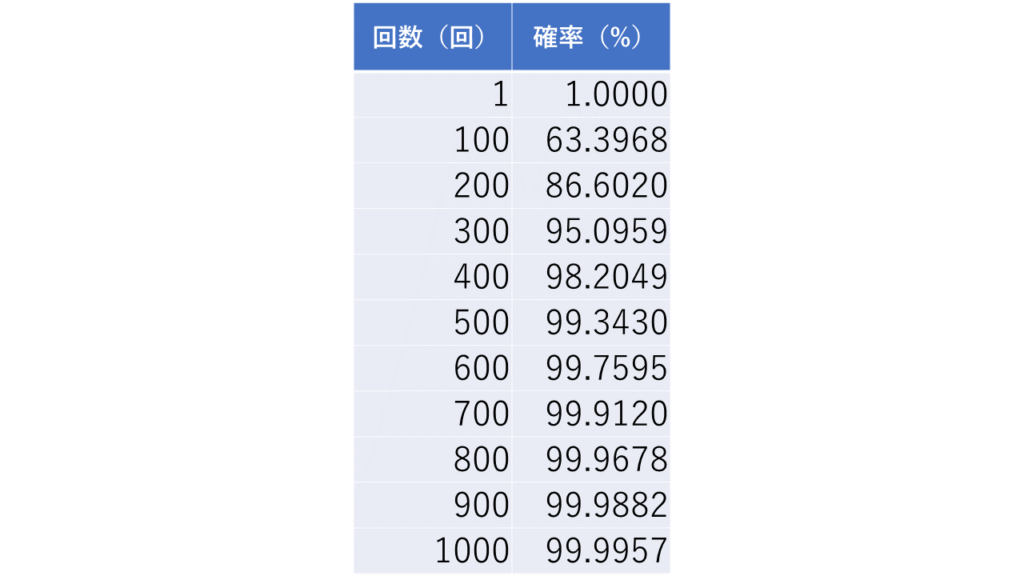
だいたい400回から500回くらいで上がりきって、それ以降は小数点第何位というレベルしか変化がないことがわかります。
なので400回くらいやったら確率的には1回はほぼ当たると言えるのではないでしょうか。
まとめ
ということで1%を100回やっても確率は100%にならない問題を取り上げてきましたが、いかがだったでしょうか。
数学的な内容って直観とずれることもあって面白いなと思います。
たまには身近なことを数学的に考えてみても面白いかもしれませんね。