パラドックスを感じる確率問題「モンティ・ホール問題」 【理系雑学】
中学の時に数学で確率の授業を受けたと思いますが、今でも内容覚えてますか?
個人的には数学の中で数少ない生活に役立つ知識だと思います。
そんな確率の問題で、今回はちょっと変わったものをご紹介しようと思います。
それは「モンティ・ホール問題」というもので、実はこれ数学界で大論争を巻き起こした問題なんです。
内容自体はとても単純なものなのですが、結論が直観とかけ離れているため起こる、いわゆるパラドックスを感じることができます。
モンティ・ホール問題の由来
モンティ・ホール問題(Monty Hall problem)とは昔アメリカで放送されていたクイズ番組で出た確率の問題です。
ちなみにその番組の司会者がモンティ・ホール(Monty Hall)さんだったことから名前がついています。
モンティ・ホール問題とは
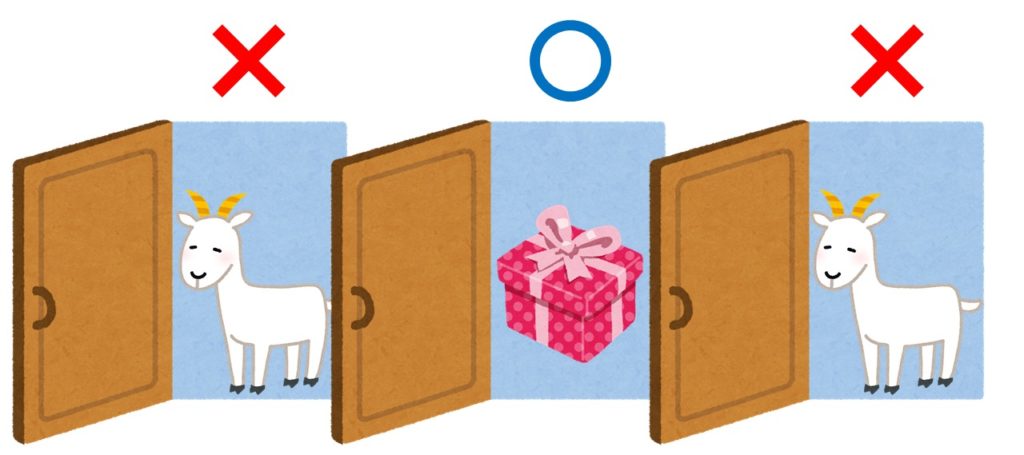
3つのドアがあり、その中の1つには当たりのプレゼントが、残りの2つにはハズレのヤギが入っています。(なんでヤギなのかは知りません)
挑戦者はその中から1つのドアを選び、プレゼントの入ったドアを開けるとそのプレゼントが手に入ります。

ここからがちょっと特殊です。
挑戦者がドアを選んだ後に、司会者は残ったドアのうちハズレの入ったドアを1つ開きます。
そして
「選択したドアを変更しますか?」
と聞きます。
挑戦者は最初に選んだドアを変更しないか、残りのもう1つのドアに変更するかを選ぶことができます。
この時に挑戦者はドアを変更すべきか、すべきでないかという確率の問題です。
ドアを変更すべきか?
この場合3つの可能性が考えられます。それは、
・ドアを変更する方が当たる確率が高い
・ドアを変更しない方が当たる確率が高い
・変更してもしなくても確率は変わらない
の3つです。
結論は「ドアを変更した方が当たる確率が高い」です。
なんと当たる確率は変更しない場合の2倍になります。
と言われてもピンときませんよね。
なぜドアを変更すると当たる確率が上がるのか?
それでは場合分けして考えてみましょう。
最初の選択したドアによる場合分け

最初にあたりのドアを選んでいた場合は、ドアを変更しなければあたり、変更すればハズレです。
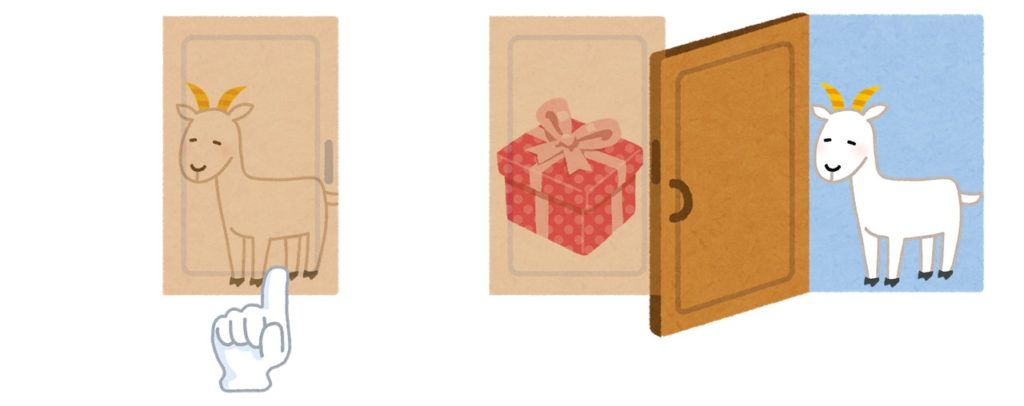
最初にハズレのドアを選んでいた場合は、ドアを変更しなければハズレ、変更すればあたりです。
「ん?どっちも2つのドアから1つを選ぶので、確率は$\frac{1}{2}$じゃないの?」
って思いませんか?私は思いました。
最初のドアの選び方
もう少し広い視野で問題を見てみましょう。
それは最初のドアの選び方です。

最初に選んだドアがあたりの確率は$\frac{1}{3}$、ハズレの確率は$\frac{2}{3}$です。
これは感覚的にもすぐに納得できると思います。
ではこれを先ほどのドアを変更するかの場合分けに当てはめてみます。
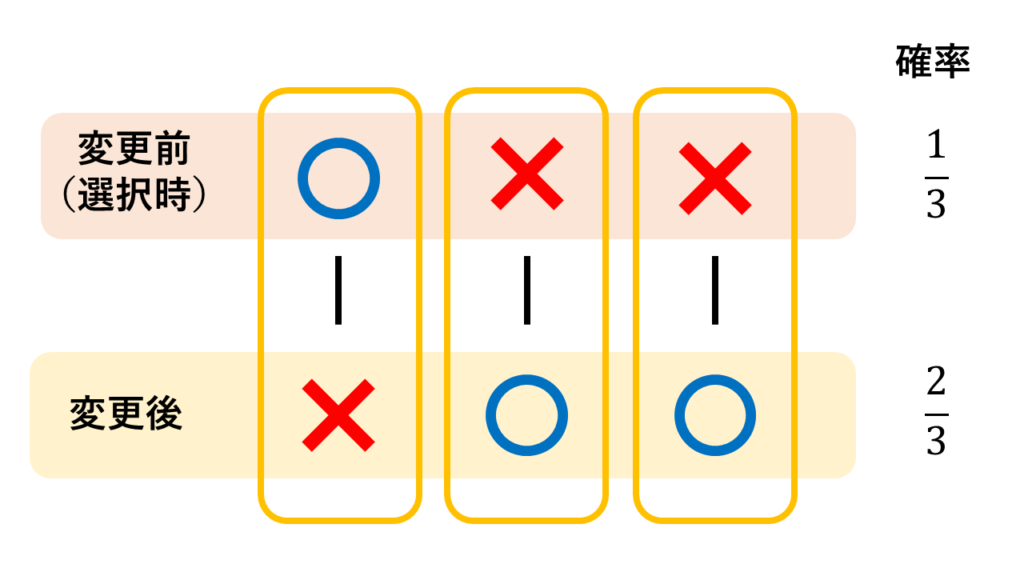
最初に選んだドアから変更しない場合が上、変更した場合が下の結果になります。
そうなんです、変更した方が当たる確率が高くなるんです。
理由はドアを変更した場合、最初に選択したドアと逆の結果が出るためです。
つまり
・最初にあたりを選んでいた場合→変更するとハズレ
・最初にハズレを選んでいた場合→変更するとあたり
となります。
そして上で解説したように、最初の選択肢ではあたりの確率$\frac{1}{3}$に対してハズレは$\frac{2}{3}$なので、ハズレの方が2倍の確率になります。
なのでこれらの2つを組み合わせると、変更した方が当たる確率が2倍になるのです。
パラドックス
どうでしょうか、ご納得いただけましたか?
結論としては上の内容が正しいです、でもピンとこないというか間違っているような気がする方もいらっしゃるのではないでしょうか?
実際この問題に関しては数学界で大論争になったらしいです。
当時マリリン・ボス・サバント(Marilyn vos Savant)さんという女性のコラムニストがドアを変更した方が当たる確率が2倍になると投稿したところ、多くの読者や数学者から批判の声が上がりました。
最終的にはコンピュータの実験によってマリリンさんが正しいと証明されたのですが、数学者という数学の専門家でさえ結論を正しいと思えなかったのです。
このような感覚・直観(推論)とは違う受け入れがたい結論が得られることを「パラドックス」と言います。
まとめ
いかがでしたでしょうか。
今回ご紹介したモンティ・ホール問題は、単純な内容なのに感覚的になかなか受け入れがたいという面白さがあります。
この他にもパラドックスは様々なものがあります。
もし興味を持っていただけたら、ネットで調べてみるとたくさん出てきますので面白いと思います。