なぜ「ゼロ割」はダメなのか?【理系雑学】
「ゼロ割はできない」ということ自体は結構有名だと思います。
ですが、なぜゼロ割はできないのでしょうか?
なんとなく知られているゼロ割について、今回は簡単にご紹介します。
なぜ「ゼロ割」はだめなのか?
私は言いやすいので「ゼロ割」と言っていますが、正式には「ゼロ除算」というみたいです。
ちなみに英語だと「division by zero」というそうです。そのままですがかっこいいです。
これ自体は簡単で、なにかを0で割り算することを指します。
例えば $1 \div 0$ みたいな感じですね。
小学校的に言えば「1の中に0は何個あるか?」という意味になりますが、この時点で意味が分からないですよね。ある意味これがゼロ割のダメな理由です。
ゼロ割がダメなのかの正解を先に書いてしまうと、ゼロで割ると無限に発散してしまうためです。
って書いてもあんまりピンときませんよね。
もう少し詳しく説明していきます。
ゼロ割が無限に発散する理由
カッコよく「無限に発散」とか書きましたが、簡単に言うと計算結果が無限になってしまってジャストな値が定まらないというイメージです。
ゼロ割を理解するために、割り算の関係についておさらいします。
まずは下の計算を見てください。
$1 \div 10 = 0.1$
$1 \div 1 = 1$
$1 \div 0.1 = 10$
$1 \div 0.01 = 100$
割る数字が小さくなればなるほど計算結果が大きくなるのがわかると思います。
この時点で割る数字をどんどん小さくしていくと、計算結果がどこまでも大きくなりそうなイメージがつきますね。
それでは次に $y = \frac{1}{x} $ のグラフを見てみます。
これは $1 \div x$ の計算結果がy軸(縦方向)になっているグラフです。
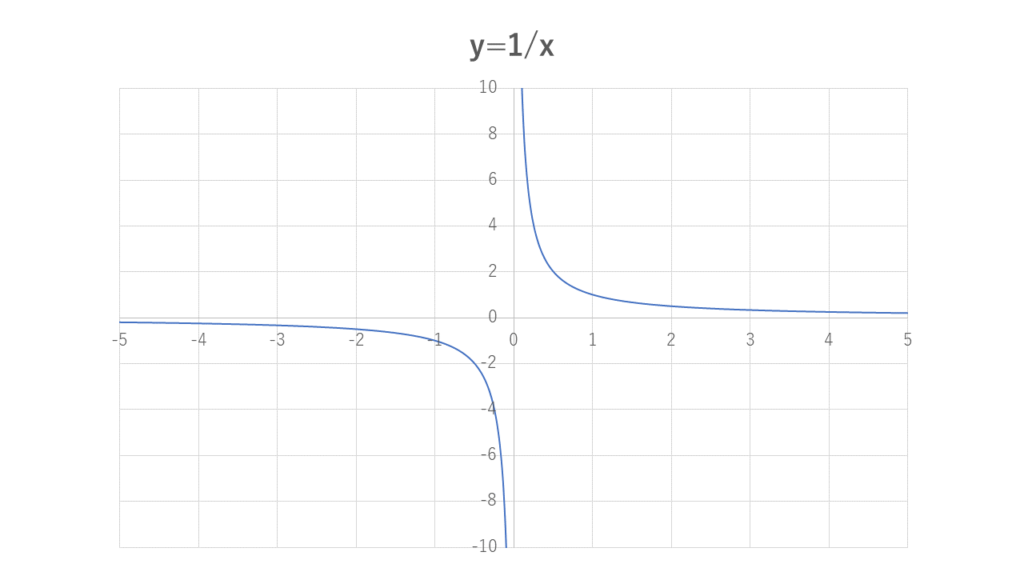
いかがでしょうか。
先ほどまで考えていたのは右上の方の線になります。
割る数字(x)が小さくなるほど計算結果(y)が大きくなっていて、割る数字が0に近づくと計算結果は見えなくなってしまっています。
これはどこまでも大きくなってしまい、無限まで行ってしまっているためです。
ちなみに左下の方の線は負の数字(マイナス)で割り算をした場合のグラフです。
これは中学数学の復讐ですが、プラスとマイナスの割り算の結果はマイナスになりますよね。
その結果このようなグラフになります。
グラフの左右どちら側から0に近づくかによって正負どちらの無限に発散するかが変わりますが、どちらにしろ無限に発散してしまうことがお分かりいただけたでしょうか。
これらのことから、0で割ったときには1つの値に定めることができないため、ゼロ割はできないのです。
まとめ
なんとなく0で割ってはいけないというのはご存じだったと思いますが、理由はイメージつきましたでしょうか?
実は世の中のいろいろなものがゼロ割を防止する機能を備えています。
例えばスマホの電卓アプリで $1 \div 0$ をするとエラーが出るはずです。
プログラムを書くときにバグが出る初歩的なものとしてもゼロ割があります。
ゼロ割は気にならない方が大半でしょうが、実はいろんなところで関係しているんです。
どんなところに潜んでいるのか考えてみても面白いかもしれません。