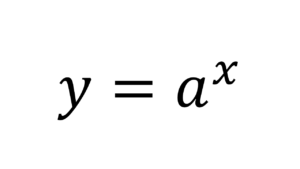なぜ0乗は1になるの? 【理系雑学】
「0乗が1になる」というのは数学では常識というか、そういうものとして学校で教えられてきたと思います。
私も学生の時は「そういうもの」として深く考えなかったのですが、最近になってなんでだろうと疑問が出てきたのでいろいろ考えてみました。
ということで、今回は0乗に関して証明を通してご説明していきます。
べき乗
0乗について考える前に、まずはそもそも「○○乗」というのはというところを簡単にご紹介します。
これはべき乗と言って、基本的には同じ数字を重ねて掛け算することです。
(「-2乗」だったり「1/2乗」、「π乗」などもあるので、単純な重ねがけだけの意味ではありませんが、今回は説明を省きます。)

べき乗はこのような形で書くことができます。
「a」は基数と呼ばれ、ここでは基準となる数字だと思ってもらって大丈夫です。
「n」は指数と呼ばれ、整数の場合は基数「a」を何回掛け算するかという意味になります。
ちなみに上のような場合は「aのn乗」と呼びます。
例えば基数が3のときの例は以下のようになります。
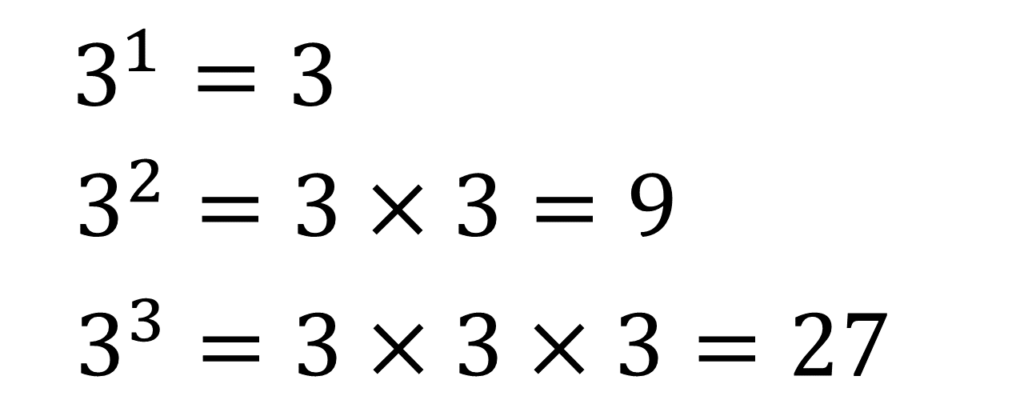
これがべき乗の基本的なところになります。
そして今回の本題ですが
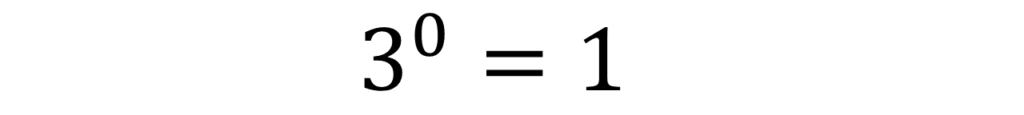
このように0乗は1になるのです。
これは基数が3のときに限らず、どんな数字でもこのようになります。
べき乗の計算による証明
それでは0乗が1になることの証明をしてみます。
まずは先ほどの3のべき乗を見直してみます。
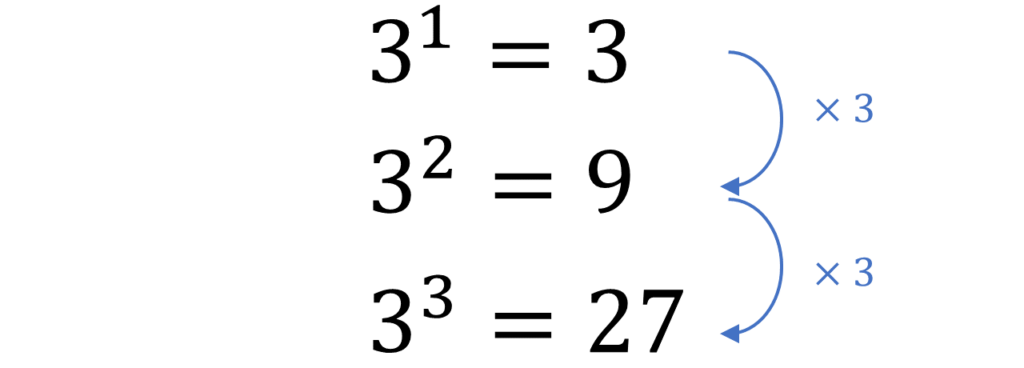
1乗、2乗、3乗を見比べてみると指数が1つ上がると3倍されているということがわかります。
すなわち指数が1つ大きくなると基数倍されているということです。
次にこれを逆側から見てみましょう。
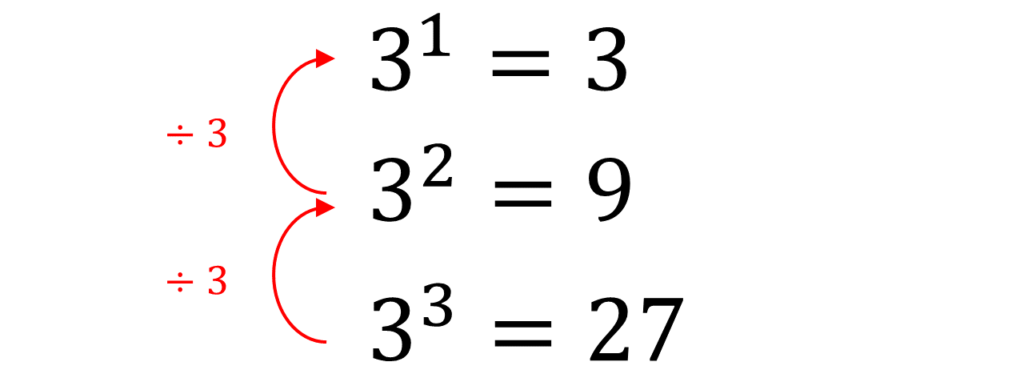
当たり前ですが指数が1小さくなるごとに3(基数)で割られています。
いかがでしょうか、何か気づきませんか?
今回最後に証明したいのは「0乗が1になる」ということですが、このまま1乗からもう1つ指数を小さくしてみたらどうなるでしょうか?
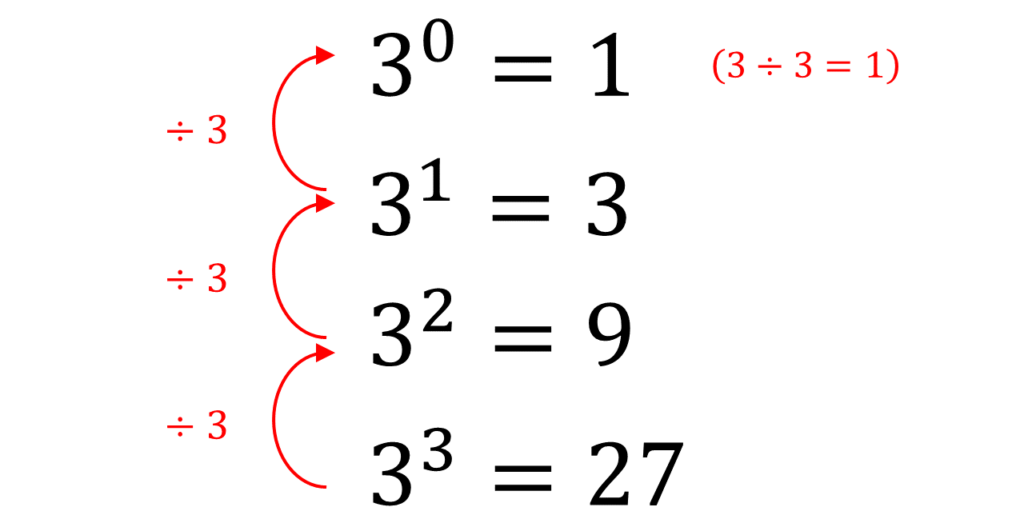
こんな風になります。
これも当たり前ですが、3を3で割るので1になります。
これは基数が3でなくても同じになるので、これで「0乗は1になる」ということの証明ができました。
0の0乗
上の内容で「0乗が1になる」ことはわかったのですが、「0の0乗」だけはちょっと勝手が違います。
0の0乗は「1」だったり「定義さない」だったりと場合によって違うというか、正直私にはどっちが正しいのかわかりません。
「0の0乗」でネットで調べてみるとたくさん記事が出てきます。興味がある方は調べてみてください。
まとめ
ということで「0乗は1になる」ということを簡単な証明を通してご説明していきましたが、ピンときましたでしょうか?
「0の0乗」に関してはちゃんとご説明ができなくてすみません。
いろいろ調べたんですが、私の中では理解しきれませんでした…
学校で「そういうもの」としか教えてもらっていないものも、理由を知るとより一層理解が深まって面白いと思います。
昔教わったことで疑問を持ったことを調べてみるといいかもしれません。